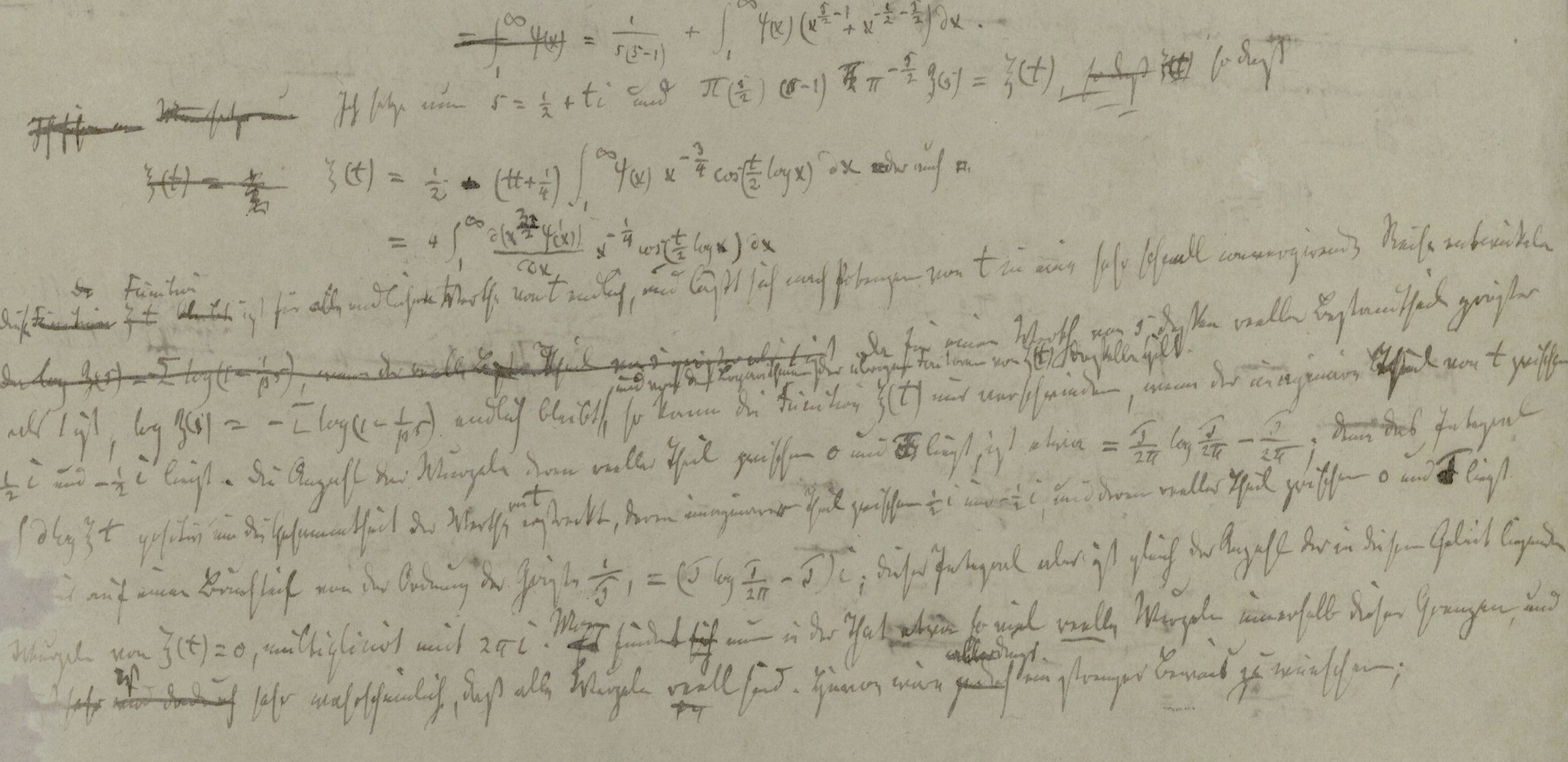
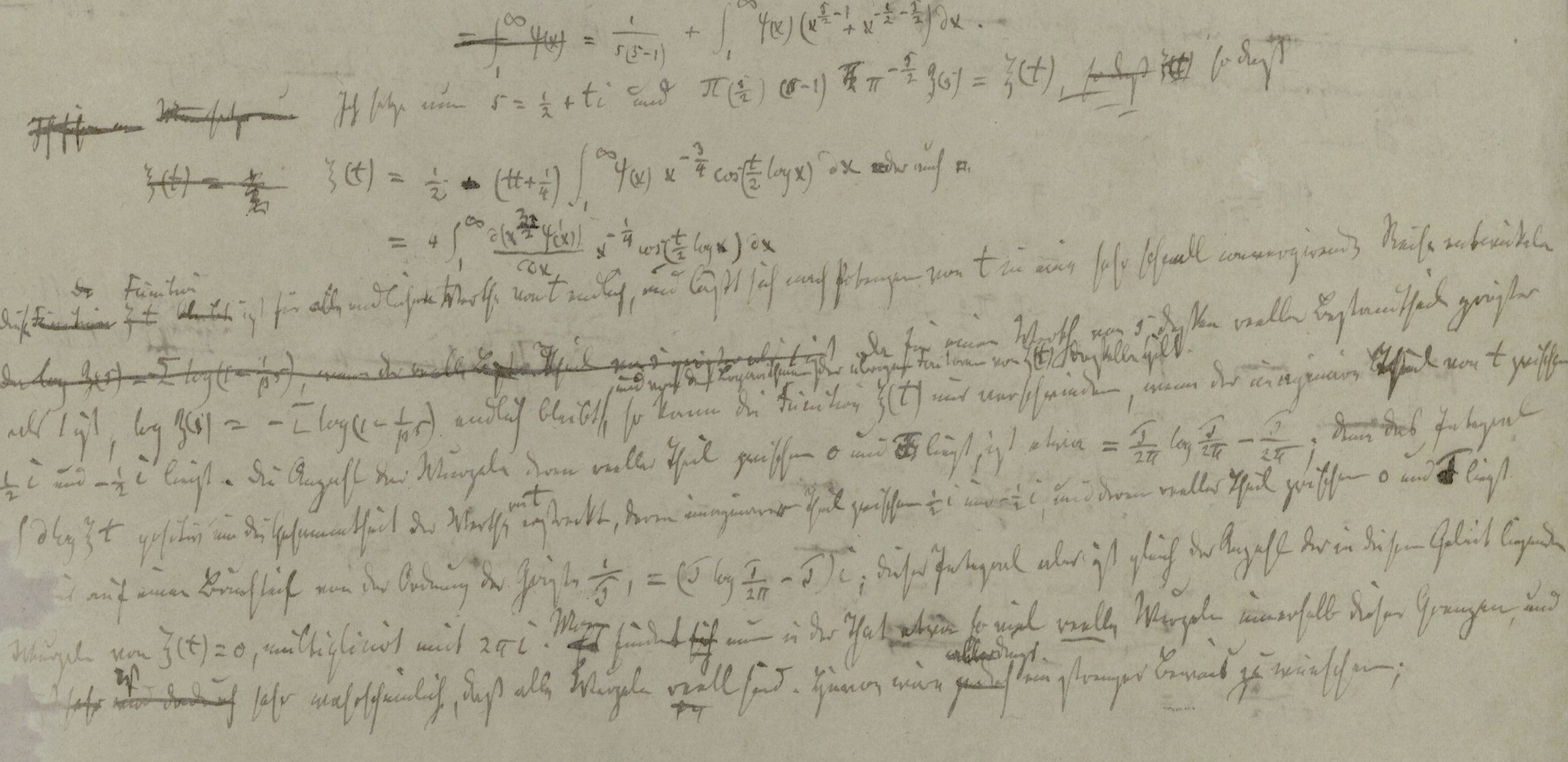
For almost 160 years, the Riemann hypothesis has been one of mathematics most famous unsolved problems. Every so often, a new mathematician arrives on the scene having developed a working proof to the hypothesis, but none have succeeded thus far in drafting up a widely-accepted solution.
Our latest contender, however, isn’t just some newbie looking to make a name for themselves. On Monday, Sir Michael Francis Atiyah, a retired and well-renowned mathematician from the UK, delivered a talk at the Heidelberg Laureate Forum where he outlined what he claimed was a proof of the Reimann hypothesis. If Atiyah’s work holds up to scrutiny, it would be a pretty wild and unexpected conclusion that earns him $1 million in prize money.
Unfortunately, that’s a big “if.”
The Riemann hypothesis is famous for what it might mean for prime numbers: natural numbers greater than one that cannot be formed by multiplying two smaller natural numbers, and therefore are only divisible by themselves or by one. Prime numbers include 2, 3, 5, 7, 11, 13, 17, 19, 23, and so forth. As you march up the number line, prime numbers are found with much less frequency and with much larger intervals spacing them apart.
Unfortunately, prime numbers don’t follow a regular pattern that lets you easily figure out what the next one will be. Just because you know that 23 is a prime number doesn’t automatically tell you that 29 is prime number, or that 31 comes after that. There’s no discernible connection between them.
In 1859, German mathematician Bernhard Riemann came up with the Riemann hypothesis, which posits that an equation known as the Riemann zeta function can accurately take a complex number (numbers that utilize both real and imaginary numbers), and deliver another number. Riemann hypothesized that the zeta function would only deliver a value of zero under certain conditions, such as plugging in a negative even integer or a complex number where the real part was 1/2.
If this hypothesis is true, the zeta function could basically identify the distribution of all prime numbers ad infinitum. While the zeta function checks out for the first 10 trillion prime numbers, the problem is still technically unsolved since you have to identify the prime number first, and then reverse engineer things to show the zeta function holds up. A proof of the Riemann hypothesis would basically be the map to the El Dorado of the math world, if you replace gold with prime numbers.
And of course, it helps that the incentives to solve the Riemann hypothesis include a $1 million prize granted under the Millennium Prize Problems, a contest to solve one of seven big math mysteries, sponsored by the Clay Mathematics Institute. People aren’t just in this for the bragging rights.
“Nobody believes any proof of the Riemann hypothesis because it is so difficult,” Atiyah said during his talk. “Nobody has proved it, so why should anybody prove it now? Unless, of course, you have a totally new idea.”
Atiyah’s proof utilizes a seemingly unrelated physics concept, the fine-structure constant, which describes the interaction of electromagnetic forces between two particles. Atiyah solves (i.e. proves) the Riemann hypothesis by “contradiction,” a kind of proof that involves assuming the problem at hand is untrue, and trying to prove it by showing that these assumptions themselves are impossible.
Many mathematicians are wary of Atiyah’s proof, for multiple reasons. There’s nothing inherently wrong with the “contradiction” approach, but it also doesn’t inspire a radical amount of confidence. There’s some evidence the fine-structure constant is capable of changing during certain conditions, and if this “constant” is inconsistent, it may not be totally appropriate to use as part of this type of proof. Atiyah’s approach seems to attempt to marry parts of particle physics with mathematics in ways that might not necessarily be compatible. A five-page writeup of his proof hinges a lot on theoretical research that has been submitted to the Proceedings of the Royal Society A, but has not been published yet—which makes it difficult for other experts to evaluate.

This is compounded by the fact that Atiyah has pitched other mathematical proofs in the last several years that could not withstand more meticulous scrutiny, causing concern that his Reimann hypothesis proof is just the latest misguided attempt.
Atiyah, who has won both the prestigious Fields Medal and Abel Prize, isn’t exactly fazed by these criticisms. “The Riemann hypothesis has been proved, unless you’re the type of person who doesn’t believe in proof by contradiction,” he said during his talk. “People usually accept proof by contradiction, so I would argue my case that I deserve the prize.” Atiyah did not respond to requests for direct comment.
Nicholas Jackson, a mathematician at the University of Warwick in the UK, says he’s “cautious at the moment” due to the lack of a rigorous peer review so far for Atiyah’s work. While acknowledging Atiyah is a “brilliant and very eminent mathematician,” Jackson emphasizes the Riemann hypothesis is “a notoriously difficult problem that has resisted solution for over a hundred and fifty years. A number of other top-rate mathematicians have nearly proved it over the last century and a half, only for a subtle but fatal flaw to be found in their proof. There’s a little poem, or ‘grook,’ by the Danish mathematician Piet Hein that says, ‘problems worthy of attack prove their worth by fighting back,’ and this is certainly true for the Riemann hypothesis.”
Furthermore, the stakes aren’t exactly sky high. If Atiyah’s proof really is true, it would be a laudable achievement, but it doesn’t necessarily do much for the rest of the mathematics community. “As many people have pointed out, the Riemann hypothesis by itself does not have spectacular consequences,” says Kenneth Ribet, a mathematician at the University of California, Berkeley. There are some modern cryptographic systems that use prime distributions to secure internet communications, but solving the hypothesis is more of an obsession local to mathematics than anything else.
“At the moment, we don’t really know enough of the details of Atiyah’s work to really make an informed decision,” says Jackson. “So I think it’s natural that the default position be a skeptical one. Mathematics relies entirely on rigorous, formal proof. Every step in the argument must be secure and robust; otherwise, the whole thing falls apart.”
