

What does math look like to mathematicians? It’s very simple. Math looks like language.
A funny language, I’ll admit. It’s dense, terse, and painstaking to read. While I zip through five chapters of a Twilight novel, you might not even turn the page in your math textbook. This language is well suited to telling certain stories (e.g., the relations between curves and equations), and ill-suited to others (e.g., the relations between girls and vampires). As such, it’s got a peculiar lexicon, full of words that no other tongue includes. For example, even if I could translate a0 + ∑ ∞ n=1 (an cos(nπx/L) + bn sin(nπx/L) into plain English, it wouldn’t make sense to someone unfamiliar with Fourier analysis, any more than Twilight would make sense to someone unfamiliar with teenage hormones.

But math is an ordinary language in at least one way. To achieve comprehension, mathematicians employ strategies familiar to most readers. They form mental images. They paraphrase in their heads. They skim past distracting technicalities. They draw connections between what they’re reading and what they already know. And—strange as it may seem—they engage their emotions, finding pleasure, humor, and squeamish discomfort in their reading material.
Now, this brief chapter can’t teach fluent math any more than it could teach fluent Russian. And just as literary scholars might debate a couplet by Gerard Manley Hopkins or the ambiguous phrasing of an email, so mathematicians will disagree on specifics. Each brings a unique perspective, shaped by a lifetime of experience and associations.
That said, I hope to offer a few nonliteral translations, a few glimpses into the strategies by which a mathematician might read some actual mathematics. Consider it Squiggle Theory 101.
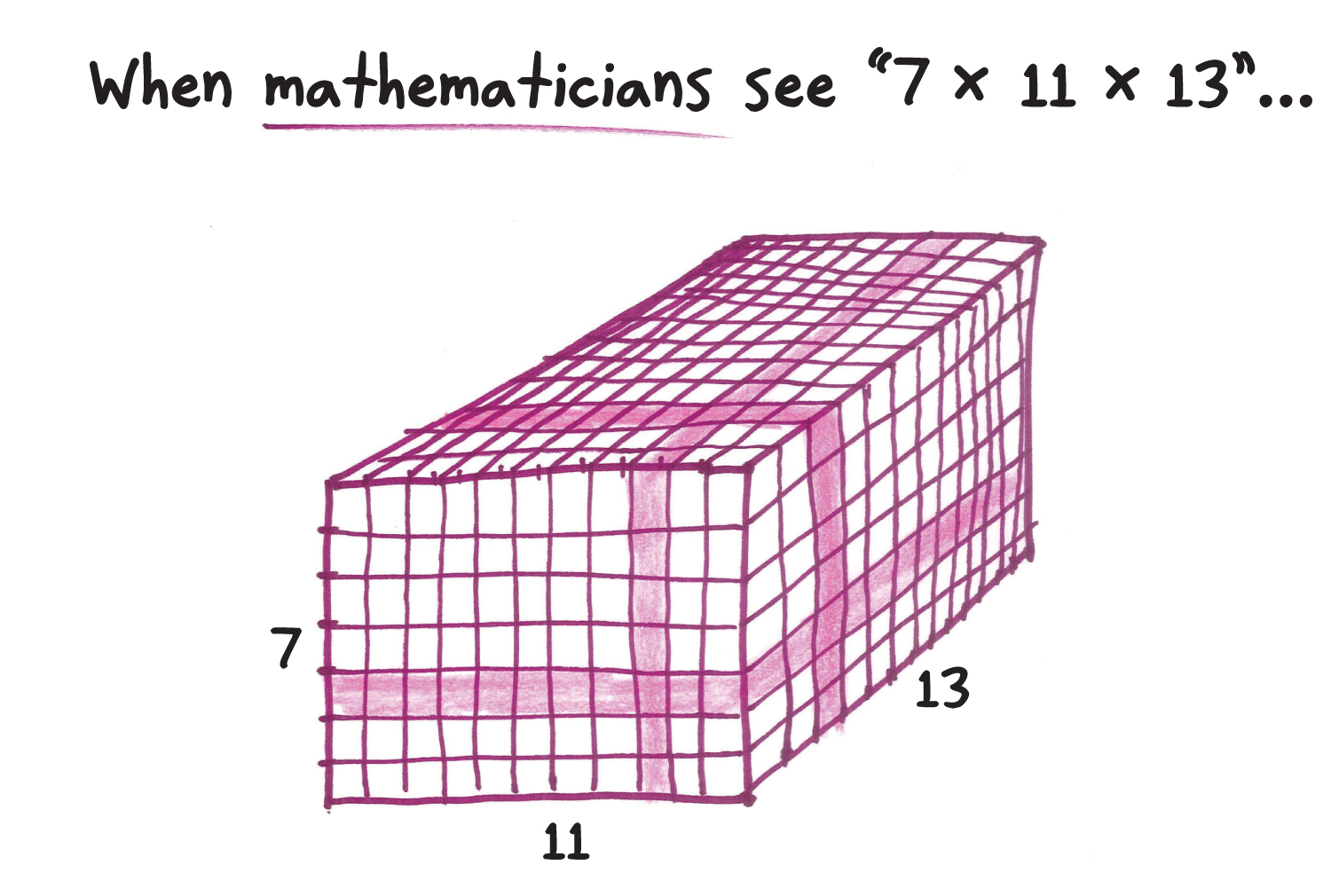
A common question I get from students: “Does it matter whether I multiply by 11 or 13 first?” The answer (“no”) is less interesting than what the question reveals: that in my students’ eyes, multiplication is an action, a thing you do. So one of the hardest lessons I teach them is this: Sometimes, don’t.
You don’t have to read 7 × 11 × 13 as a command. You can just call it a number and leave it be.
Every number has lots of aliases and stage names. You could also call this number 1002 – 1, or 499 × 2 + 3, or 5005/5, or Jessica, the Number That Will Save Planet Earth, or plain old 1001. But if 1001 is how this number is known to its friends, then 7 × 11 × 13 isn’t some quirky and arbitrary moniker. Rather, it’s the official name you’d find on the birth certificate.
7 × 11 × 13 is the prime factorization, and it speaks volumes.
Some key background knowledge: Addition is kind of boring. To wit, writing 1001 as the sum of two numbers is a truly dull pastime: you can do it as 1000 + 1, or 999 + 2, or 998 + 3, or 997 + 4 . . . and so on, and so on, until you slip into a boredom coma. These decompositions don’t tell us anything special about 1001, because all numbers can be broken up in pretty much the same way. (For example, 18 can be written as 17 + 1, or 16 + 2, or 15 + 3 . . . ) Visually, this is like breaking a number up into two piles. No offense, but piles are dumb.
Multiplication: now that’s where the party’s at. And to join the festivities, you need to deploy our first math-reading strategy: forming mental images.
As the picture on the previous page shows, multiplication is all about grids and arrays. 1001 can be seen as a giant structure of blocks, 7 by 11 by 13. But that’s just getting started.
You can visualize this as 13 layers of 77 each. Or, if you tilt your head sideways, it’s 11 layers of 91 each. Or, tilting your head a different sideways, seven layers of 143 each. All of these ways to decompose 1001 are immediately evident from the prime factorization . . . but virtually impossible to discern from the name 1001 without laborious guesswork.
The prime factorization is the DNA of a number. From it, you can read all the factors and factorizations, the numbers that divide our original and the numbers that don’t. If math is cooking class, then 7 × 11 × 13 isn’t the pancake recipe. It’s the pancake itself.

To casual fans, π is a mystic rune, a symbol of mathematical sorcery. They ponder its irrationality, memorize thousands of its digits, and commemorate Pi Day on March 14 by combining the most glorious of mankind’s arts (dessert pies) with the least glorious (puns). To the general public, π is an object of obsession, awe, even something approaching worship.
And to mathematicians, it’s roughly 3.
That infinite spool of decimal places that so captivates laypeople? Well, mathematicians aren’t that bothered. They know math is about more than precision; it’s about quick estimates and smart approximations. When building intuition, it helps to streamline and simplify. Intelligent imprecision is our next crucial math-reading strategy.
Take the formula A = πr2, which many students have heard so often the mere phrase “area of a circle” triggers them to scream, “Pi r squared!” like sleeper agents programmed by brainwashing. What does it mean? Why is it true?
Well, forget the 3.14159. Let your mind go fuzzy. Just look at the shapes.
r is the radius of our circle. It’s a length.
r2, then, is the area of a little square, like the one pictured.
Now, the π-dollar question: How does the area of the circle compare to the area of the square?
Clearly, the circle is bigger. But it’s not quite four times bigger (since four squares would cover the circle and then some). Eyeballing it, you might speculate that the circle is a little more than three times bigger than the square.
And that’s exactly what our formula says: Area = a little more than 3 × r².
If you want to verify the precise value—why 3.14-ish and not 3.19-ish?—then you can use a proof. (There are several lovely demonstrations; my favorite involves peeling the circle like an onion and stacking the layers to make a triangle.) But mathematicians, whatever they insist, don’t always prove everything from first principles. Like everyone from carpenters to zookeepers, they’re happy to employ a tool without knowing precisely how it was constructed, so long as they have a sense of why it works.
Excerpted from Math with Bad Drawings by Ben Orlin. September 2018, Black Dog and Leventhal Publishers. Published with permission.
