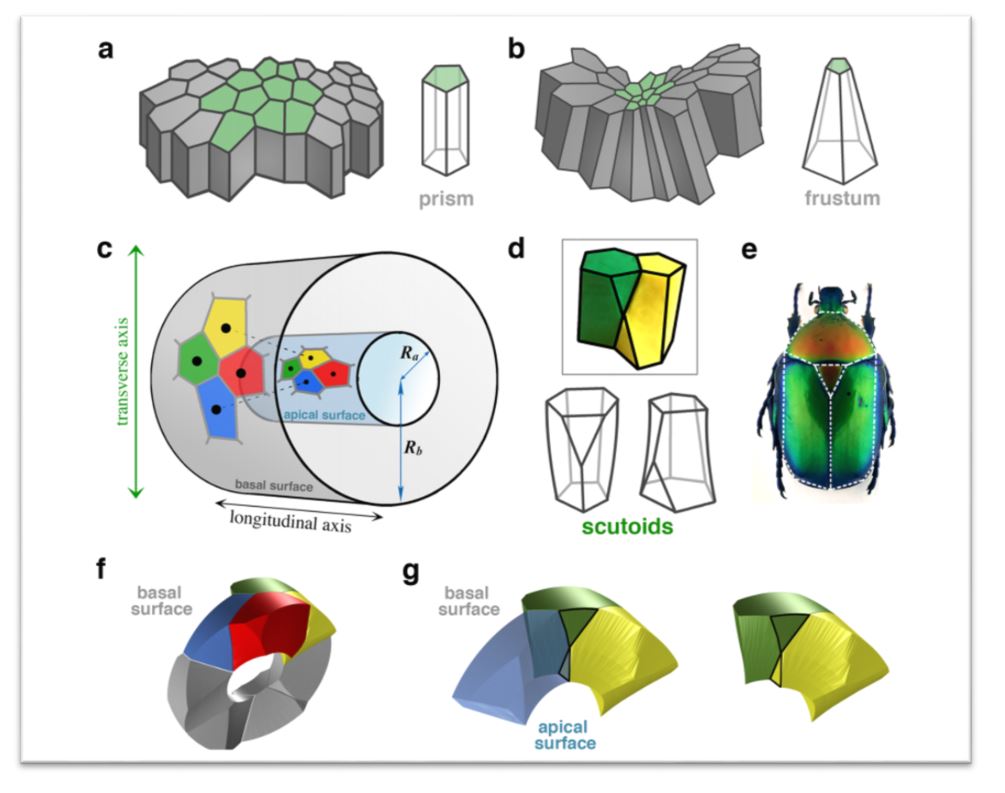

“Scientists just discovered a new shape” makes for a great headline—and a lot of questions. Chief among them: What the heck is a new shape? How can a shape be new? Surely all shapes exist, at least in theory, and we’re just coming along and describing them. And while we’re on that note, what even is a shape?
The paper that sparked all these questions, published in Nature Communications this week, indeed reports a new shape called a “scutoid” in the epithelial cells making up human skin. It looks a bit like a column with one corner chopped off. It also seems to be somehow relevant to biological membranes and cellular function, but I was too boggled by the whole new shape concept to even begin wrapping my mind around the medical implications.
Google had no answers to offer. “How can there be a new shape?” Nothing. “What is a new shape?” Nada. “How can shapes be new?” Every query just turned up more headlines, none of them attached to stories that solved the mystery. It just made no sense to me. Shapes don’t get discovered—they just are. Right? Right??
Lost, frustrated, and losing hope that I’d ever find an answer that wasn’t Wikipedia’s pathetic definition of “shape,” I started emailing mathematicians. Thankfully, they had some answers.
“The question ‘Can there be new shapes?’ depends, as you realized, on the meaning of ‘new’ and ‘shape’,” says Matthew Gursky, a professor of mathematics at the University of Notre Dame. For the purposes of their article, he went on, the authors of the Nature Communications paper defined a shape as any body that occupies three-dimensional space, such as a cake or a rock (his examples, not mine). Gursky says mathematicians might not necessarily use “shape” in that way, but that that’s not really relevant—what matters is how the paper defines it. The paper is interested in talking about how the scutoid is relevant to biological objects like epithelial cells.
So is this shape really new? “It depends what you mean,” he says. “If by ‘new’ you mean that it didn’t exist before (like a new model of car), then the answer is ‘no,’ of course. What they mean by “new” is a shape that has never been mathematically described and studied.” It’s possible, of course, that someone else in some other discipline has described and studied the scutoid. Gursky notes that what’s new in one field can be well-known in another. “The same equations that describe the shape of soap bubbles also describe the shape of black holes, for example.”
To me, it makes no sense to say that something is “new” if you just happened to be the first person to describe it. I realize that by that argument there are no new species (barring those that evolve into distinct, previously nonexistent species)—there are only newly discovered species. To that I say: yes. I think that finding out about a frog that you didn’t know about before doesn’t make it new—it just makes it new to you.
So I asked the authors of the paper how a shape could possible be new. Surely there are already infinite shapes out in the world and we were merely coming along to describe them.
“There are indeed infinite forms,” says Javier Buceta, one of the study authors. We discover some of those shapes through practical uses, he says, like finding out about circles via the wheel. “Our research is sort of connected to that, because the scutoid was found in connection with a fundamental problem about how cells pack together to make tissues and organs, and until now nobody thought about it because there was no need to.”
Similarly, he says, the number 3.14159… (and so on) always existed, but at some point someone came along and called it pi because it became useful to give it a name and describe its features. Scutoids, like pi, are now of scientific interest, and so someone needed to come along to describe their features and give them a name.
All of this describing and naming only matters, though, if there is some larger issue at stake. “In the abstract, there may not be much to say about these particular shapes,” says Burt Totaro, a professor of mathematics at UCLA, “but the authors do have a point to make.” In a biological context like the epithelium, he notes, “it’s not good enough to think of cells as having a simpler geometric shape such as a prism or frustum (a slice of a cone). The outer surface and the inner surface of the cell are typically being squeezed in different directions, and so more complicated shapes arise inevitably.” If you’re interested in modeling how biological membranes work, then, you need to find a way to mathematically describe this “new” “shape,” and it’s pretty convenient to give it a name as well.
So, yes, as Buceta himself confirmed, the scutoid shape clearly already existed. In that sense it’s not “new.” And maybe it’s not even what some mathematicians would call a “shape.” But for the purposes of talking about mathematical descriptions of a three-dimensional object that’s suddenly become biologically relevant, let’s call it a new shape. Welcome to the world, little buddy.
